Base 2
Contents
Definition
Base 2, also known as Binary, is a method of counting wherein a radix, or base, of 2 is used. Radix or base is the number of unique digits, including zero, that are used to represent numbers. In Binary, only 0 and 1 are used to represent numbers.
What does this mean
When thinking of base 2, think about exponents of 2. So 2^2 = 4, 2^3 = 8, so on and so forth. If exponents are hard to understand, just imagine 2 being multiplied by itself x number of times. x can represent any number or exponent (the formal term). To elaborate on this, starting from the right-most digit, the power 2 is raised to will be 0. As you go further left, the power is raised further. For example, in a 4-digit number in binary, the left-most digit will represent 2^3 which is 8. This corresponds to 1000 in binary (base 2) being equal to 8 in decimal (base 10).
Relevance
Explanation
Base 2 is the base we use for exponents. In terms of binary data storage, base 2 is the standard counting system we use for calculating the number of patterns a data storage contains. For example: 8-bits of data store 256 patterns of data because the 8 added to the power of 2 (2^8) is 256.
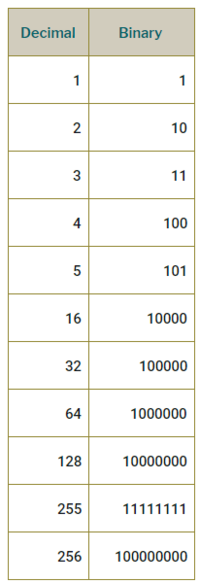
Base 2 Table
See also
External Links
https://en.wikipedia.org/wiki/Binary https://www.khanacademy.org/math/algebra-home/alg-intro-to-algebra/algebra-alternate-number-bases/v/number-systems-introduction